笔记 | (1)分治算法

EthanCao

参考教材: 算法导论

EthanCao

分治算法递归式

分解: 将问题分解为多个子问题
解决: 递归地求解每个子问题
合并: 将子问题的解合并为原问题的解

T(n)=\begin{cases} \Theta(1) & n\leq c \\[0ex] a_1T(n/b_1)+\cdots+a_kT(b_k)+f(n) & n>c \end{cases}
递归式: 分别生成a_i个规模为n/b_i的子问题, 合并与分解需要f(n)

1-代入法

简化递归式: 进行合适的变量代换
猜测解的形式: 使用递归树预测, 逐步缩小解的范围
用数学归纳法证明: 可以适当添加低阶项进行放缩

示例1: T(n)=4(n/2)+n

猜测(1): T(n)=O(n^3)
假设: \forall t<n,T(t)\leq ct^3
证明: T(n)=4T(n/2)+n\leq 4c(n/2)^3+n=cn^3/2+n\leq cn^3
满足: n\geq\sqrt{2/c}

猜测(2): T(n)=O(n^2)
假设: \forall t<n,T(t)\leq ct^2+dt
证明: T(n)=4T(n/2)+n\leq 4c(n/2)^2+4d(n/2)+n=cn^2+(2d+1)n\leq cn^2+dn
满足: d\leq-1

猜测(3): T(n)=\Omega(n^2)
假设: \forall t<n,T(t)\geq ct^2
证明: T(n)=4T(n/2)+n\geq 4c(n/2)^2+n=cn^2+n\geq cn^2
综上所述: T(n)=\Theta(n^2)

示例2: T(n)=2T(\sqrt{n})+\lg n
变量代换: m=\lg n\iff 2^m=n
新递归式: T(2^m)=2T(2^{m/2})+m
变换形式: S(m)=2S(m/2)+m
得到结果: T(n)=S(m)=\Theta(m\lg m)=\Theta(\lg n\lg\lg n)

2-递归树法

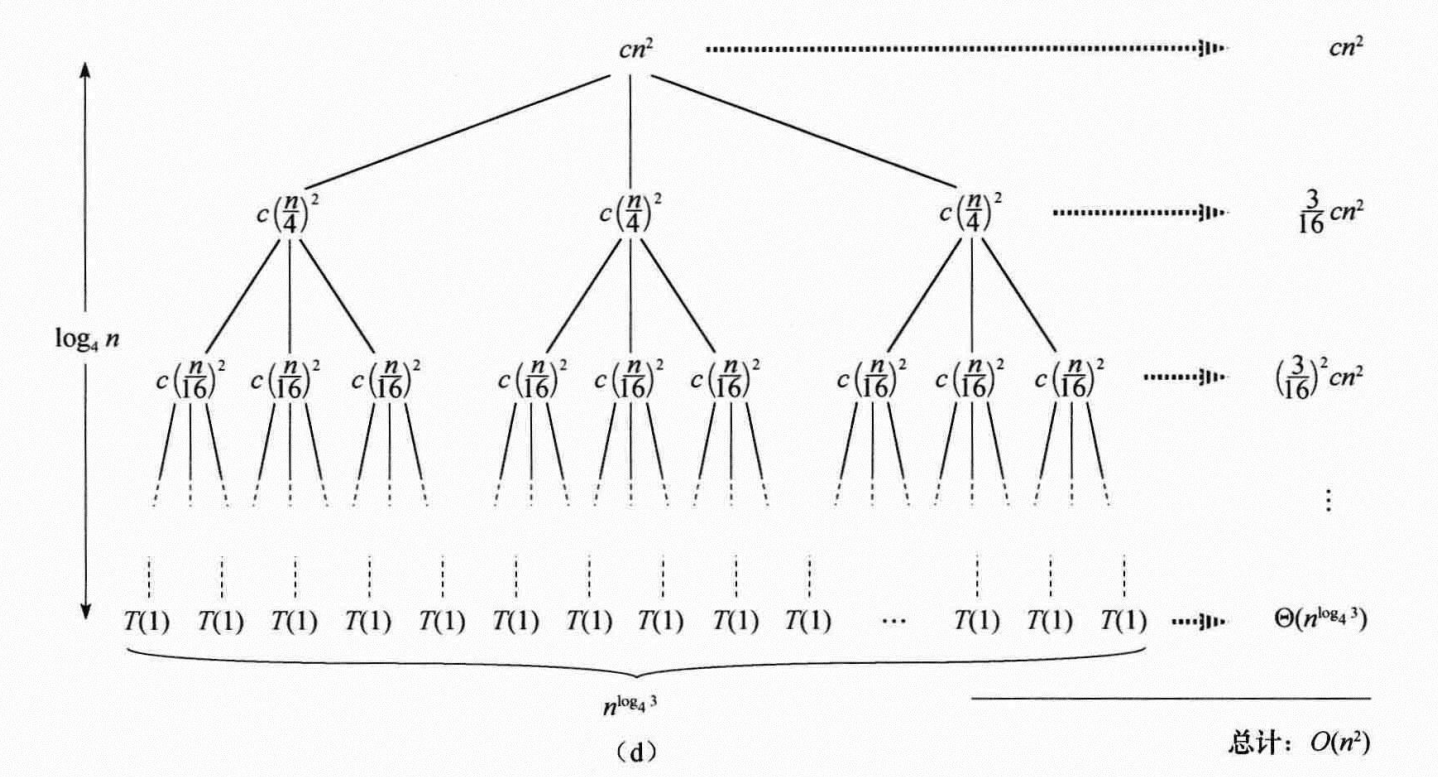
递归式1: T(n)=3T(n/4)+\Theta(n^2)
\begin{aligned} 由递归树得\quad T(n)&=cn^2+(3/16)cn^2+\cdots+(3/16)^{\log_4n-1}cn^2+\Theta(n^{\log_43}) \\ &=cn^2\cdot\sum_{i=0}^{\log_4n-1}(3/16)^i+\Theta(n^{\log_43}) \\ &=cn^2\cdot\frac{1-(3/16)^{\log_4n}}{1-3/16}+\Theta(n^{\log_43})=O(n^2) \end{aligned}
根节点复杂度为cn^2\implies T(n)=\Omega(n^2)\implies T(n)=\Theta(n^2)

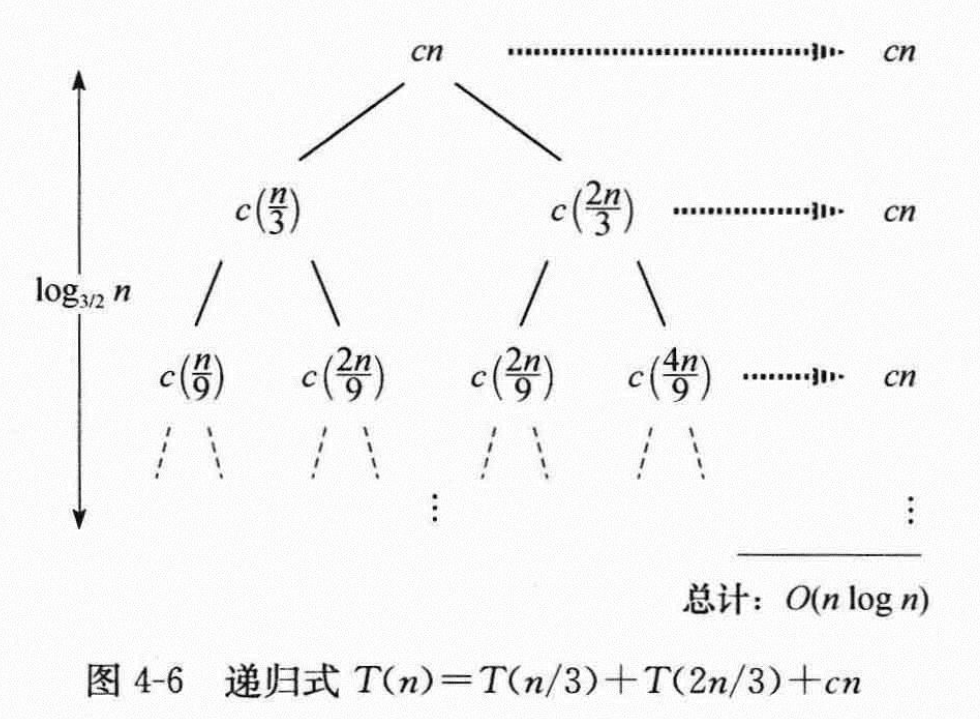
递归式2: T(n)=T(n/3)+T(2n/3)+O(n)
每层代价: \leq cn
最短层数: \log_3n
最长层数: \log_{3/2}n
得到下界: \Omega(cn\cdot\log_3n)=\Omega(n\lg n)
猜测上界: O(cn\cdot\log_{3/2}n)=O(n\lg n)

代入法证明: 假设 \forall t<n,T(t)\leq dn\lg n
\begin{aligned} T(n)&=T(n/3)+T(2n/3)+O(n) \\ &\leq T(n/3)+T(2n/3)+cn \\ &\leq d(n/3)\lg(n/3)+d(2n/3)\lg(2n/3)+cn \\ &=dn\lg n-dn(\lg3-2/3)+cn\leq dn\lg n \end{aligned}

3-主定理

引理1: 用递归树化简递归式

引理1: 已知 a\geq1,b>1,f(n):\{b^i\}\mapsto\mathbb{R^+}
\begin{aligned} T(n)&=\begin{cases}\Theta(1) & n=1 \\ aT(n/b)+f(n) & n=b^i \end{cases} \\ &=\sum_0^{\log_b n-1}a^if(n/b^i)+\Theta(n^{\log_b a}) \end{aligned}

证明: 自上而下每层结点的质量呈几何衰减数量几何增加
两者此消彼长, 将共同作用的效果逐层累加得到最终结果
第\{0,1,\cdots,\log_b n-1\}层为枝结点层, 第\log_b n层为叶子层
逐层累加得 T(n)=\sum_0^{\log_b n-1}a^if(n/b^i)+\Theta(n^{\log_b a})

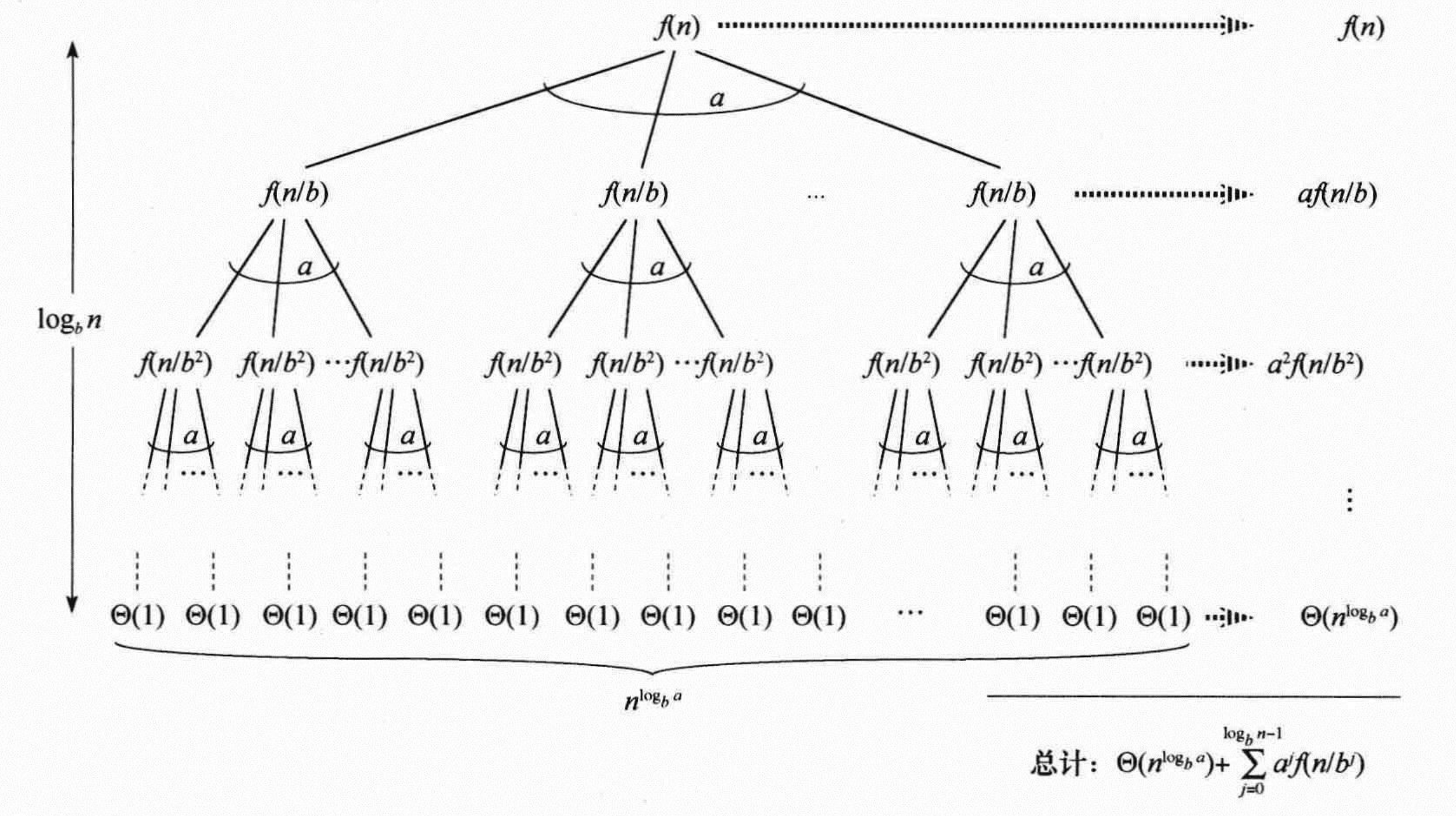
引理2: 幂次散点上的枝结点复杂度

引理2: 已知 a\geq1,b>1,f(n):\{b^i\}\mapsto\mathbb{R^+}
枝结点函数 g(n):\{b^i\}\mapsto\mathbb{R^+}:\sum_0^{\log_bn-1}a^if(n/b^i)

叶结点主导: f(n)=O(n^{\log_ba-\epsilon})\implies g(n)=O(n^{\log_ba})
各层均分布: f(n)=\Theta(n^{\log_ba})\implies g(n)=\Theta(n^{\log_ba}\lg n)
根结点主导: af(n/b)\leq cf(n)\implies g(n)=\Theta(f(n)):c<1
------

(1)叶结点主导: f(n)= O(n^{\log_ba-\epsilon})\implies g(n)=O(n^{\log_ba})
\begin{aligned} g(n)&=\sum_0^{\log_bn-1}a^if(n/b^i)\leq\sum_0^{\log_b n-1}a^i(n/b^i)^{\log_b a-\epsilon} \\ &=n^{\log_ba-\epsilon}\sum_0^{\log_bn-1}a^ib^{-i\log_ba}b^{i\epsilon}=n^{\log_ba-\epsilon}\sum_0^{\log_bn-1}a^ia^{-i}b^{i\epsilon} \\ &=n^{\log_ba-\epsilon}\sum_0^{\log_bn-1}b^{i\epsilon}\quad(取决于最后几层) \\ &=n^{\log_ba-\epsilon}\frac{b^{\epsilon\log_bn}-1}{b^\epsilon-1}=n^{\log_ba-\epsilon}\frac{n^\epsilon-1}{b^\epsilon-1} \\ &\leq n^{\log_ba-\epsilon}\frac{n^\epsilon}{b^\epsilon-1}=n^{\log_ba}\frac{1}{b^\epsilon-1}=O(n^{\log_ba}) \end{aligned}

(2)各层均分布: f(n)=\Theta(n^{\log_ba})\implies g(n)=\Theta(n^{\log_ba}\lg n)
\begin{aligned} g(n)&=\sum_0^{\log_bn-1}a^if(n/b^i)\sim\sum_0^{\log_b n-1}a^i(n/b^i)^{\log_ba} \\ &=n^{\log_ba}\sum_0^{\log_bn-1}a^ib^{-i\log_ba}=n^{\log_ba}\sum_0^{\log_bn-1}a^ia^{-i}\quad(每层一样大) \\ &=n^{\log_ba}\log_bn=\Theta(n^{\log_ba}\lg n) \end{aligned}

(3)根结点主导: af(n/b)\leq cf(n)\implies g(n)=\Theta(f(n))
\because af(n/b)\leq cf(n)\implies a^if(n/b^i)\leq c^if(n):c<1
\begin{aligned} \therefore g(n)&=\sum_0^{\log_b n-1}a^if(n/b^i)\leq\sum_0^{\log_b n-1}c^if(n)\quad(取决于最初几层) \\ &\leq f(n)\sum^\infty c^i=f(n)\frac{1}{1-c}=O(f(n))\end{aligned}
\therefore T(n)=\Omega(f(n))\implies T(n)=\Theta(f(n))

引理3: 幂次散点上的总复杂度

引理3: 已知 a\geq1,b>1,f(n):\{b^i\}\mapsto\mathbb{R^+}
总复杂度 T(n):\{b^i\}\mapsto\mathbb{R^+}:\begin{cases}\Theta(1) & n=1 \\ aT(n/b)+f(n) & n=b^i \end{cases}

叶结点主导: f(n)= O(n^{\log_ba-\epsilon})\implies T(n)=\Theta(n^{\log_ba})
每层均分布: f(n)=\Theta(n^{\log_ba})\implies T(n)=\Theta(n^{\log_ba}\log n)
根结点主导: f(n)=\Omega(n^{\log_ba+\epsilon})\land af(n/b)\leq cf(n)\implies T(n)=\Theta(f(n))

(1) T(n)=g(n)+\Theta(n^{\log_b a})=O(n^{\log_ba})+\Theta(n^{\log_b a})=\Theta(n^{\log_ba})
(2) T(n)=g(n)+\Theta(n^{\log_b a})=\Theta(n^{\log_ba}\lg n)+\Theta(n^{\log_b a})=\Theta(n^{\log_ba}\lg n)
(3) T(n)=g(n)+\Theta(n^{\log_b a})=\Theta(f(n))+O(f(n))=\Theta(f(n))

引理4: 整数集上的总复杂度

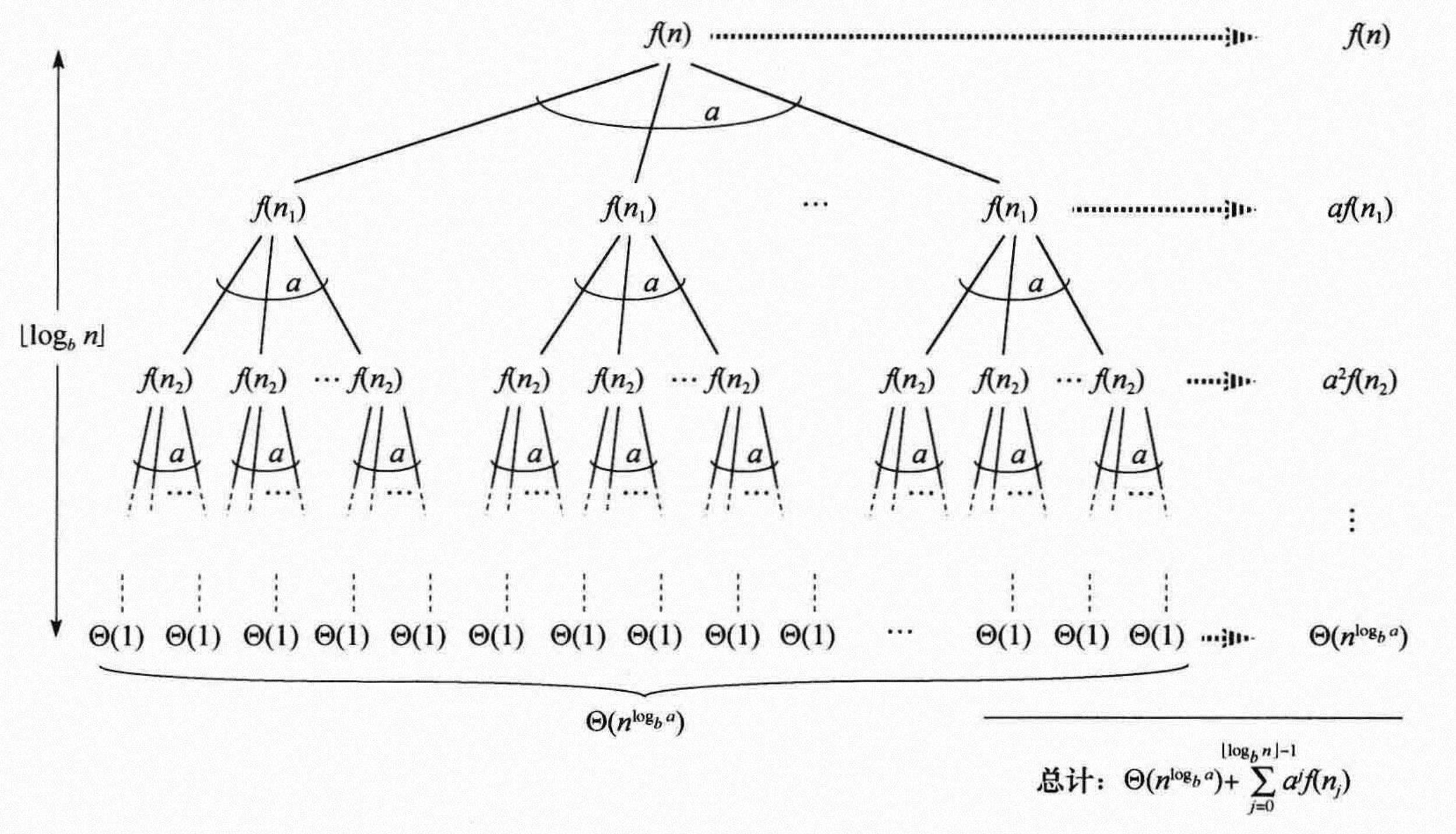
对于递归式 T(n)=aT(\lceil n/b\rceil)+f(n)
已满足下界 aT(n/b)+f(n)\leq aT(\lceil n/b\rceil)+f(n)
现欲证上界 aT(\lceil n/b\rceil)+f(n)\leq aT(n/b+1)+f(n)

枝结点层\{n_0,\cdots,n_{\lfloor\log_bn\rfloor-1}\}, 叶结点层n_{\lfloor\log_bn\rfloor}
每层结点大小 n_i=\begin{cases} n & i=0 \\ \lceil n_{i-1}/b\rceil\leq(n_{i-1}/b)+1 & i>0 \end{cases}

\left\{\begin{aligned} n_0 &\leq n \\ n_1 &\leq (n_0/b)+1=n/b+1 \\ n_2 &\leq (n_1/b)+1=n/b^2+1/b+1 \\ n_3 &\leq (n_2/b)+1=n/b^3+1/b^2+1/b+1 \\ n_i &\leq (n_{i-1}/b)+1=n/b^{i}+\sum_0^{i-1}1/b^k\leq n/b^{i}+\sum_0^\infty1/b^k=n/b^{i}+\frac{b}{b-1} \\ n_{\lfloor\log_bn\rfloor}&\leq \frac{n}{b^{\lfloor\log_bn\rfloor}}+\frac{b}{b-1}<\frac{n}{b^{\log_bn-1}}+\frac{b}{b-1}=b+\frac{b}{b-1}=O(1) \end{aligned}\right.

递归树总复杂度 T(n)=\sum_0^{\lfloor\log_bn\rfloor-1}a^if(n_i)+\Theta(n^{\log_ba})

叶结点主导: f(n)=O(n^{\log_ba-\epsilon})\overset{(1)}\implies f(n_i)=O(\frac{n}{b^i}^{\log_ba-\epsilon})\implies T(n)=\Theta(n^{\log_ba})
各层均分布: f(n)=\Theta(n^{\log_ba})\overset{(2)}\implies f(n_i)=\Theta(\frac{n}{b^i}^{\log_ba})\implies T(n)=\Theta(n^{\log_ba}\lg n)
根结点主导: f(n)=\Omega(n^{\log_ba+\epsilon})\land af(n/b)\leq cf(n)\overset{(3)}\implies T(n)=\Theta(f(n))
------

(1)叶结点主导: f(n)=O(n^{\log_ba-\epsilon})\overset{(1)}\implies f(n_i)=O(\frac{n}{b^i}^{\log_ba-\epsilon})
然后由引理3-(1)可知 T(n)=\Theta(n^{\log_ba})
\begin{aligned} f(n_i) &\leq f(n/b^{i}+\frac{b}{b-1}) \\ &\leq (\frac{n}{b^i}+\frac{b}{b-1})^{\log_ba-\epsilon} \\ &=(\frac{n}{b^i})^{\log_ba-\epsilon}(1+\frac{b^i}{n}\cdot\frac{b}{b-1})^{\log_ba-\epsilon} \\ &\leq (\frac{n}{b^i})^{\log_ba-\epsilon}(1+\frac{b}{b-1})^{\log_ba-\epsilon}=O(\frac{n}{b^i}^{\log_ba-\epsilon}) \\ \end{aligned}

(2)各层均分布: f(n)=\Theta(n^{\log_ba})\overset{(2)}\implies f(n_i)=\Theta(\frac{n}{b^i}^{\log_ba})
然后由引理3-(2)可知 T(n)=\Theta(n^{\log_ba}\lg n)
\begin{aligned} \because f(n_i) &\geq f(n/b^{i})=\Omega(\frac{n}{b^i}^{\log_ba}) \\ \because f(n_i) &\leq f(n/b^{i}+\frac{b}{b-1})=O(\frac{n}{b^i}^{\log_ba}) \\ \therefore f(n_i) &=\Theta(\frac{n}{b^i}^{\log_ba}) \end{aligned}

(3)根结点主导: f(n)=\Omega(n^{\log_ba+\epsilon})\land af(n/b)\leq cf(n)
\overset{(3)}\implies f(n_i)=\Omega(\frac{n}{b^i}^{\log_ba+\epsilon})\land a^if(n_i)\leq c^if(n)

\because\exists N_1,\forall n>N_1,af(n/b)\leq cf(n)
\implies\exists N_2>N_1,\forall n>N_2,af(n/b+1)\leq cf(n)
\implies\exists N_2>N_1,\forall n>N_2,a^if(n/b^i+\sum_0^{i-1}1/b^k)\leq c^if(n)
\implies\exists N_3>N_2,\forall n>N_3,a^if(n/b^i+\frac{b}{b-1})\leq c^if(n):c<1
\implies a^if(n_i)\leq a^if(n/b^i+\frac{b}{b-1})\leq c^if(n)
由引理3-(3)可知 T(n)=\Theta(f(n))

EthanCao

示例:归并排序

def MERGE(A, lBin, rBin, rEnd):
    L = A[lBin:rBin]  # A[lBin, rBin)
    R = A[rBin:rEnd]  # A[rBin, rEnd)
    L.append(float("inf")) # 大值哨兵
    R.append(float("inf")) # 大值哨兵

    i, j = 0, 0
    for k in range(lBin, rEnd):
        if L[i] <= R[j]:
            A[k] = L[i]
            i += 1
        else:
            A[k] = R[j]
            j += 1

# 处理范围: A[bin, end-1]
def MERGE_SORT(A, bin, end):
    if bin < end - 1:
        mid = (bin + end) // 2
        MERGE_SORT(A, bin, mid)
        MERGE_SORT(A, mid, end)
        MERGE(A, bin, mid, end)

无大值哨兵版本

def MERGE(A, lBin, rBin, rEnd):
    L = A[lBin:rBin]  # A[lBin, rBin)
    R = A[rBin:rEnd]  # A[rBin, rEnd)

    # 循环处理直到一侧耗尽
    i, j, k = 0, 0, lBin
    while i < len(L) and j < len(R):
        if L[i] <= R[j]:
            A[k] = L[i]
            i += 1
        else:
            A[k] = R[j]
            j += 1
        k += 1
    
    # 处理剩余部分
    if i < len(L):
        A[k:rEnd] = L[i:]
    elif j < len(R):
        A[k:rEnd] = R[j:]

可行性分析

起始: 只含1个元素的组是有序的
递推: 已知A[lBin, rBin)和A[rBin, rEnd)是有序的
由MERGE过程可知, 合并后的A[lBin, rEnd)也是是有序的
结束: 最终得到的A[0, len(A))有序, 即整个数组有序

时间复杂度分析

分解: 只需计算中间位置mid, 时间复杂度\Theta(1)
解决: 递归解决两个规模减半的子问题, 时间复杂度2T(n/2)
合并: 合并两个规模为n/2的有序数组, 时间复杂度\Theta(n)

T(n)=\begin{cases} \Theta(1) & n=1 \\[0ex] 2T(n/2)+\Theta(n) & n>1 \end{cases}\implies(n^{\log_22}\sim n)\implies\Theta(n\lg n)

EthanCao

示例: 最大子数组

def FIND_MAX_CROSSING_SUBARRAY(A, bin, mid, end):
    """返回包含中间元素的最大子数组[mBin, mEnd)"""
    sum = 0
    lSum = -float("inf")
    for i in range(mid - 1, bin - 1, -1):  # [mid-1, bin]
        sum = sum + A[i]
        if sum > lSum:
            lSum = sum
            lIdx = i

    sum = 0
    rSum = -float("inf")
    for j in range(mid, end):  # [mid, end)
        sum = sum + A[j]
        if sum > rSum:
            rSum = sum
            rIdx = j

    return lIdx, rIdx + 1, lSum + rSum


def FIND_MAXIMUM_SUBARRAY(A, bin, end):
    """返回最大子数组[xBin, xEnd)->xSum"""
    if bin == end - 1:
        return bin, end, A[bin]
    else:
        mid = (bin + end) // 2
        lBin, lEnd, lSum = FIND_MAXIMUM_SUBARRAY(A, bin, mid)  # [bin, mid)
        rBin, rEnd, rSum = FIND_MAXIMUM_SUBARRAY(A, mid, end)  # [mid, end)
        mBin, mEnd, mSum = FIND_MAX_CROSSING_SUBARRAY(A, bin, mid, end)

        sum = max(lSum, rSum, mSum)
        if sum == lSum:
            return lBin, lEnd, lSum
        elif sum == rSum:
            return rBin, rEnd, rSum
        else:
            return mBin, mEnd, mSum

T(n)=\begin{cases} \Theta(1) & n=1 \\[0ex] 2T(n/2)+\Theta(n) & n>1 \end{cases}\implies(n^{\log_22}\sim n)\implies\Theta(n\lg n)

EthanCao

示例: 斐波那契数列

直接代入公式

import math
def FIB_FORMULA(n):
    pos = (1 + 5 ** 0.5) / 2
    neg = (1 - 5 ** 0.5) / 2
    return int((pos ** n - neg ** n) / math.sqrt(5))

\begin{aligned} F(n)=\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right] \end{aligned}

直接递归

def FIB_RECURSION(n):
    if n in [0, 1]:
        return n
    return FIB_RECURSION(n - 1) + FIB_RECURSION(n - 2)

T(n)=T(n-1)+T(n-2)+1\implies\Theta((\frac{1+\sqrt{5}}{2})^n)

用变量代换证明:

递推: T(n)=T(n-1)+T(n-2)+1
\implies T(n)+1=[T(n-1)+1]+[T(n-2)+1]
\implies A(n)=A(n-1)+A(n-2)
初始: A(0)=T(0)+1=2, A(1)=T(1)+1=2
最终: A(n)=\frac{2}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right]=\Theta((\frac{1+\sqrt{5}}{2})^n)

用递归树证明:
每个叶节点贡献值为1, 故需要的叶结点总数为F(n)
递归过程中将所有叶节点两两相加, 因此需要F(n)-1次加法操作

动态规划

def FIB_DP(n):
    if n in [0, 1]:
        return n

    dp = [0, 1] + [0] * (n-1)
    for i in range(2, n + 1):
        dp[i] = dp[i - 1] + dp[i - 2]
    return dp[n]

矩阵快速幂

def FIB_MATRIX_POWER(n):
    if n in [0, 1]:
        return n

    F = np.array([[1, 1], 
                  [1, 0]])
    return np.linalg.matrix_power(F, n - 1)[0][0]

起始: \begin{bmatrix}a_2&a_1\\a_1&a_0\end{bmatrix}=\begin{bmatrix}1&1\\1&0\end{bmatrix}
递推: \begin{bmatrix}1&1\\1&0\end{bmatrix}\begin{bmatrix}a_n&a_{n-1}\\a_{n-1}&a_{n-2}\end{bmatrix} =\begin{bmatrix}a_n+a_{n-1}&a_{n-1}+a_{n-2}\\a_n&a_{n-1}\end{bmatrix} =\begin{bmatrix}a_{n+1}&a_{n}\\a_{n}&a_{n-1}\end{bmatrix}
最终: \begin{bmatrix}a_n&a_{n-1}\\a_{n-1}&a_{n-2}\end{bmatrix}=\begin{bmatrix}1&1\\1&0\end{bmatrix}^{n-1}

EthanCao

示例: 峰值查找(一维, 二维)

def PEAK_SEARCH_1D(A, offset=0):
    """返回峰值索引及其值"""
    n = len(A)
    if n == 1:
        return offset, A[0]
    if n == 2:
        if A[0] > A[1]:
            return offset, A[0]
        else:
            return offset + 1, A[1]

    mid = n // 2
    # 左侧比中点大, 继续搜索左侧
    if A[mid - 1] > A[mid]:
        return PEAK_SEARCH_1D(A[0:mid], offset)
    # 右侧比中点大, 继续搜索右侧
    elif A[mid + 1] > A[mid]:
        return PEAK_SEARCH_1D(A[mid + 1 : n], offset + mid + 1)
    # 中点即为峰值, 直接返回
    else:
        return offset + mid, A[mid]

时间复杂度: T(n)=T(n/2)+\Theta(1)\implies(n^{\log_21}\sim1)\implies\Theta(\lg n)

def PEAK_SEARCH_2D(A: np.array, offsetX=0):
    """返回2D网格中的峰值坐标及其值"""
    n = len(A)
    if n in [1, 2]:
        maxX, maxY = np.unravel_index(np.argmax(A), A.shape)
        return maxX + offsetX, maxY, A[maxX][maxY]

    midX = n // 2
    maxY = np.argmax(A[midX])
    # 上侧比中轴最值更大, 继续搜索上侧
    if A[midX - 1][maxY] > A[midX][maxY]:
        return PEAK_SEARCH_2D(A[:midX], offsetX)
    # 下侧比中轴最值更大, 继续搜索下侧
    elif A[midX + 1][maxY] > A[midX][maxY]:
        return PEAK_SEARCH_2D(A[midX + 1 :], offsetX + midX + 1)
    # 中轴最值即为峰值, 直接返回
    else:
        return midX + offsetX, maxY, A[midX][maxY]

时间复杂度: T(n)=T(n/2)+\Theta(m)\implies\Theta(m\lg n)